Guaranteed Self-Triggered Control of Disturbed Systems: A Set Invariance Approach
Jun 3, 2025·
,
,
,
,
,
,
,
·
0 min read
Florian Pouthier
Sylvain Durand
Nicolas Marchand
Jonathan Dumon
Abdoullah Ndoye
Amaury Negre
Pierre Susbielle
Jose J. Castillo-Zamora
J. Fermi Guerrero Castellanos
Franck Ruffier
Abstract
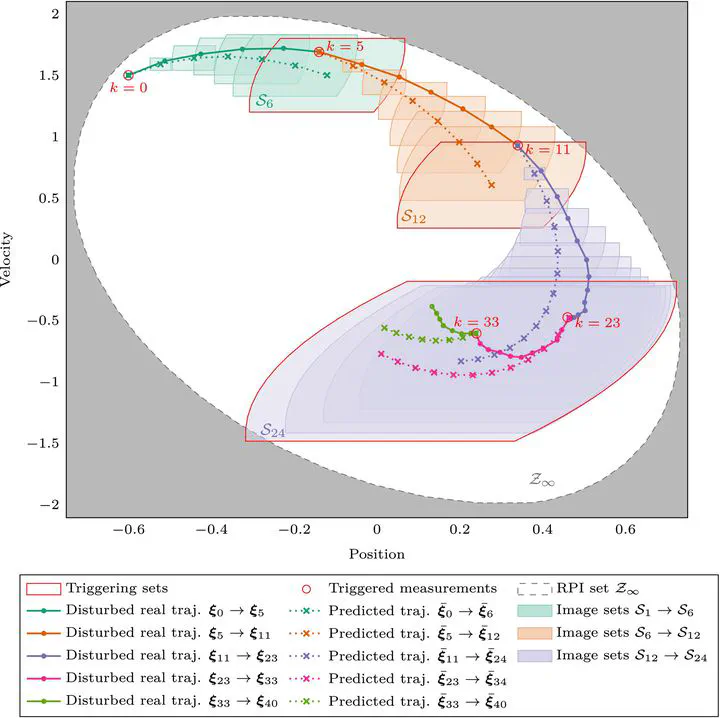
This article introduces a novel self-triggering strategy designed to ensure the control of discrete-time linear systems with guaranteed stability, even in the presence of disturbances and uncertainties. This strategy aims to consistently maintain satisfaction of state constraints while accounting for the uncertainties in the system through a set-membership description. The self-triggering framework primarily relies on reachable and invariant sets. Reachable sets quantify the maximum deviation of the disturbed system from the predicted behavior, while an invariant set establishes triggering bounds for these reachable sets. This control method is intended to minimize the number of measurements required, thereby avoiding network bandwidth saturation. To validate the effectiveness of the proposed strategy, the experiments are conducted on an air extractor system, demonstrating a reduction in the number of measurement samples while ensuring stability and satisfying system state constraints.
Type
Publication
International Journal of Robust and Nonlinear Control, 1(1)
Status
Peer-reviewed
Open access
License
CC-BY-4.0
Authors
Doctor in Control and Robotics
My research focuses on the efficient navigation of UAVs in constrained environments. I recently joined the LEASARD CominLabs project at LS2N Nantes, in which I investigate SLAM and navigation algorithms with event-based cameras to improve drone autonomy in cluttered environments. This work is supervised by Isabelle Fantoni. My Ph.D. thesis work, led at ICube Strasbourg and GIPSA-lab Grenoble, has been dedicated to the event-driven navigation of a drone in dark environments, as a part of the dark-NAV ANR project. This thesis has been supervised by Nicolas Marchand and Sylvain Durand. Through my research work, I developed research interests in aerial robotics, robust control and set theory. As a graduate of an engineering school (INSA Strasbourg), I have developed a taste for control theory, which I try to deploy as much as possible on real control systems.
